Matematica finanziaria in pillole (3^ Parte)

di Marco Salvaterra

3^ Parte: REINTEGRAZIONE e AMMORTAMENTO

Glossario:
Reintegrazione: in economia la quota di reintegrazione è la somma che si deve accantonare annualmente in previsione di dover sostenere una spesa futura per la sostituzione di un mezzo di produzione fisso (che dura più cicli); in matematica finanziaria, la reintegrazione è l’inverso dell’accumulazione finale.
Ammortamento: ripartizione in valori annui di un determinato capitale iniziale. In matematica finanziaria, l’ammortamento è l’inverso dell’accumulazione iniziale. La rata annua di ammortamento è la somma pagata ogni anno per estinguere un debito in un certo numero di anni.

Formule inverse della annualità:
a) Reintegrazione
b) Ammortamento

a) Formula di reintegrazione
Mediante questa formula (inversa della formula di accumulazione finale di annualità) è possibile determinare la somma che, accantonata annualmente per un certo numero di anni pari a n, permette di avere una determinata somma (A_n) al termine del periodo. Viene utilizzata anche per calcolare la media economica (ad. es. il reddito medio annuo posticipato Bfm di beni che danno redditi poliennali (boschi) o variabili annualmente (frutteti).

Formula di reintegrazione

dove:
a = somma annua
A_n = somma riferita alla fine del periodo

Esercizio 1.
Una macchina agricola viene acquistata al prezzo di € 40.000. La sua durata in efficienza è prevista per 800 ore di funzionamento e nell’azienda essa sarà impiegata per 100 ore all’anno. Nell’ipotesi che sia realizzabile un valore di recupero pari al 10% del valore a nuovo, se ne calcoli la quota annua di reintegrazione (Q_a), dato un saggio di interesse del 5%.

Durata = 8 anni
Valore da reintegrare = 40.000 – 4.000 = 36.000

Q_a = 36.000 x 0,05/(1,05⁸ – 1) = 3.769,98 €

b) Formula di ammortamento
Questa formula, detta anche di estinzione di un capitale, serve per calcolare la rata costante di ammortamento di un mutuo. Ogni rata risulta formata dalla quota d’interesse sul capitale prestato e dalla quota capitale che serve per rimborsare via via il debito. La rata di ammortamento risulta costante, mentre la quota interessi diminuisce con il decrescere del debito, mentre la quota capitale aumenta.

Formula di ammortamento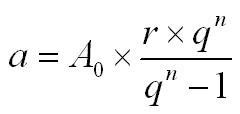

n = numero di annualità
a = rata annua di ammortamento
A₀ = debito iniziale

Esercizio 2.
Per l’acquisto di un immobile viene contratto un mutuo decennale di 100.000 € al tasso del 5,0%, estinguibile con rate annue di ammortamento.
Calcolare la rata annua.

Rata annua = 100.000 x (0,05 x 1,05¹⁰)/(1,05¹⁰ – 1) = 12.950,46 €

Se il mutuo viene estinto con rate che maturano più volte in un anno (es. semestrali o mensili), dovrà essere utilizzata la stessa formula con l’avvertenza di dividere il saggio di interesse per t (t = numero di rate all’anno) e moltiplicare il numero di anni n sempre per t.

Esercizio 3.
Per l’acquisto di un immobile viene contratto un mutuo ventennale di 100.000 € al tasso del 5,0%, estinguibile con rate semestrali di ammortamento.
Calcolare la rata semestrale.

Rata semestrale = 100.000 x (0,025 x 1,025⁴⁰)/(1,025⁴⁰ – 1) = 3.983,62 €

Debito residuo di un mutuo
Il piano di ammortamento di un mutuo riporta anche il debito che resta da estinguere dopo aver pagato le singole rate. Qualora di debba calcolare il debito residuo dopo aver pagato un certo numero di rate, si dovrà accumulare (attraverso la formula di accumulazione iniziale di annualità limitate) le rate che devono essere ancora pagate.

Esercizio 4.
Viene acceso un mutuo ventennale di 80.000 € da estinguere con rate semestrali al saggio del 5%.
Calcolare l’importo che deve essere pagato (Debito residuo Dr) qualora si voglia estinguerlo anticipatamente quando sta per scadere la quindicesima rata.

Rata semestrale = 3.186,90 €

Mancano da pagare 25 rate più la rata in scadenza.

Importo da versare (Dr) = 3.186,90 x (1,025²⁵ – 1)/(0,025 x 1,025²⁵) + 3.186,90 = 61,903,52 €

E’ possibile scaricare (cliccando qui >>>) un file in formato .xls (Microsoft Excel) che permette di calcolare il piano di ammortamento di un mutuo.
Istruzioni:
Inserire i dati nelle caselle con numeri in rosso (importo mutuo, durata in anni, saggio di interesse e numero di rate all’anno (se annue = 1, se semestrali = 2, se mensili = 12).

Matematica finanziaria in pillole (2^ Parte)

Matematica finanziaria in pillole (4^ Parte)

Marco Salvaterra, laureato in Scienze agrarie presso la Facoltà di Agraria di Bologna, insegna Estimo ed Economia agraria all’Istituto Tecnico Agrario di Firenze. Curriculum vitae >>>