Matematica finanziaria in pillole (2^ Parte)

di Marco Salvaterra

2^ Parte: VALORI PERIODICI (rendite frazionate, annualità, periodicità)

Glossario:
Valori periodici: sono somme che si ripetono ad intervalli regolari.
Rendite frazionate: valori che si ripetono ad intervalli pari a frazioni di anno (mensilità, bimestralità, semestralità, ecc.).
Annualità: valori che si ripetono ad intervalli pari a un anno.
Periodicità: valori che si ripetono ad intervalli pari a multipli di anno (ogni due anni, ogni tre anni, ecc.; il periodo è detto turno = t).
Anticipati o posticipati: i valori periodici sono anticipati o posticipati a seconda se cadono all’inizio o alla fine del periodo (es. per le mensilità – rendite frazionate – all’inizio o alla fine del mese, per le annualità all’inizio o alla fine dell’anno, per le periodicità all’inizio o alla fine del turno).
Costanti o variabili: i valori periodici sono costanti se hanno lo stesso importo.
Limitati o illimitati: se sono un certo numero di valori si dicono limitati, se se ripetono all’infinito sono illimitati.

Valori periodici:
a) Rendite frazionate (R)
b) Annualità (a)
c) Periodicità o poliannualità (P)

a) Rendite frazionate (R)
Rendite frazionate: valori che si ripetono ad intervalli pari a frazioni di anno.

Sommatoria a fine anno (S₁) delle rendite frazionate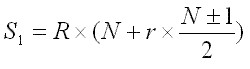

dove:
R = importo rendita frazionata
N = numero di rendite all’anno
r = saggio di interesse
± 1 = +1 se sono rendite anticipate, -1 se posticipate

Esercizio 1.
Un immobile è affittato a un canone annuo di 8.400 € pagabile con rate mensili anticipate. Calcolare l’ammontare del canone annuo posticipato (Cap). Saggio di interesse = 0,04

Cap = 700 x (12 + 0,04 x (12+1)/2) = 8.582 €

b) Annualità (a)
Annualità: valori che si ripetono ad intervalli pari a un anno.
I libri di testo riportano molte formule relative alle annualità limitate (finale, iniziale – o addirittura intermedia – di annualità posticipate e anticipate); noi preferiamo utilizzarne una soltanto, quella di accumulazione finale di annualità costanti posticipate limitate. Con questa è possibile accumulare un certo numero di annualità dove cade l’ultima e da lì, con il montante (qⁿ) o la formula inversa (1/qⁿ) è possibile riportare la somma all’istante desiderato.

Formula di accumulazione finale di annualità costanti posticipate limitate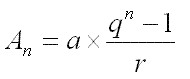

dove:
n = numero di annualità

Esercizio 2.
Tizio deposita per 5 anni, alla fine di ogni anno, 2.000 €. Calcolare a quanto ammonta il deposito complessivo due anni dopo l’ultimo deposito (r = 4%).

A₇ = 2.000 x (q⁵ – 1)/0,04 x q² = 2.000 x 5,41632256 x 1,0816 = 11716,59 €

c) Periodicità o poliannualità (P)
Periodicità: valori che si ripetono ad intervalli pari a multipli di anno (ogni due anni, ogni tre anni, ecc.; il periodo è detto turno = t).
E’ possibile ricavare le formule relative alle periodicità partendo da quelle delle annualità. Basta sostituire r con q^t – 1, e qn con q^{m x t} , dove m indica il numero di periodicità; pertanto:

Formula di accumulazione finale di periodicità costanti limitate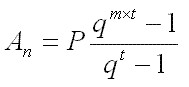

dove:
A_n = accumulazione di periodicità dove cade l’ultima
m = numero di periodicità
t = turno o periodo (n di anni tra una periodicità e l’altra)

Esercizio 3.
Calcolare l’accumulazione finale di una periodicità posticipata di 4.000 € che si ripete ogni 4 anni per 5 volte (r = 5%).

A₂₀ = 4.000 x (q²⁰ – 1)/(q⁴ – 1) = 30.686,77 €

Valori periodici illimitati
Essendo valori (annualità o periodicità) che si ripetono all’infinito, sarà possibile calcolare soltanto l’accumulazione iniziale (queste formule sono dette anche di capitalizzazione).

Accumulazione iniziale di annualità costanti posticipate illimitate

A₀ = a/r

Il caso di applicazione pratica più frequente è nella stima analitica del V₀ (V₀ = B_f/r_c), dove B_f è il Beneficio fondiario e r_c il saggio di capitalizzazione.
Come detto sopra, sostituendo r con q^t – 1, si ottiene la formula relativa alle periodicità:

Accumulazione iniziale di periodicità costanti posticipate illimitate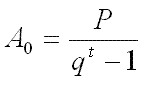

Esercizio 4.
Calcolare l’accumulazione iniziale di una serie illimitata di annualità posticipate di € 2.000, dato un saggio di interesse del 4%.

A₀ = 2.000/0,04 = 50.000 €

Esercizio 5.
Un bosco ceduo che si riproduce naturalmente, fornisce un reddito netto ogni 15 anni di 8.000 €. Calcolare il valore del bosco all’inizio del ciclo (cioè appena effettuato il taglio). (saggio di interesse 3%)

V₀ = 8.000/(1,03¹⁵ -1) = 14.337,77 €

• Matematica finanziaria in pillole (1^ Parte)
• Matematica finanziaria in pillole (3^ Parte)

Marco Salvaterra, laureato in Scienze agrarie presso la Facoltà di Agraria di Bologna, insegna Estimo ed Economia agraria all’Istituto Tecnico Agrario di Firenze. Curriculum vitae >>>