Matematica finanziaria in pillole (1^ Parte)
di Marco Salvaterra
1^ Parte: INTERESSE SEMPLICE E INTERESSE COMPOSTO
Glossario:
Capitale (C): è una somma di denaro che viene concessa in uso per un determinato tempo.
Interesse (I): è il prezzo d’uso del capitale.
Saggio o tasso di interesse (r): l’interesse prodotto dall’unità di capitale (1 euro) in un anno; è espresso in numero decimale (es. 0,05) o in percentuale (es. 5%).
Montante (M nell’interesse semplice – Cn nell’interesse composto): somma del capitale e dell’interesse prodotto in un determinato tempo.
Sconto: è il pagamento anticipato di una cambiale da parte di una banca. Con lo stesso termine si indica anche la somma che la banca si trattiene a titolo di compenso.
Note: negli esercizi gli importi in euro sono arrotondati al centesimo.
Regime di interesse:
a) Interesse semplice
b) Interesse composto:
– discontinuo annuo
– discontinuo convertibile (convertibile t volte in un anno)
a) Regime di interesse semplice
Si ha quando gli interessi maturati vengono allontanati dal capitale, che perciò rimane immutato nel tempo. Si applica per periodi inferiori o pari a un anno.
Interesse semplice (I)
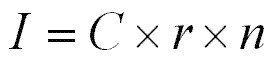
dove n è il numero di mesi diviso 12 oppure il numero di giorni diviso 365 (anno solare) o 360 (anno commerciale).
Da questa formula è possibile ricavare le formule inverse che permettono di calcolare una qualsiasi delle variabili (C, r, n) note le altre tre (le formule inverse non vengono riportate per non appesantire la trattazione).
Esercizio 1.
Calcolare l’interesse prodotto da un capitale di 6.000 Euro impiegato al tasso di interesse del 4% in tre mesi.
I = 6.000 x 0,04 x 3/12 = 60 €
Montante semplice (M) = C + I = C + C x r x n
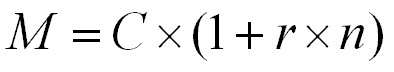
Anche in questo caso è possibile ricavare le formule inverse che permettono di calcolare una qualsiasi delle variabili (C, r, n) note le altre tre.
Esercizio 2.
Calcolare il montante prodotto da un capitale di 2.500 Euro in 6 mesi al tasso del 5%.
M = 2.500 x (1 + 0,05 x 6/12) = 2.562,50 €
b) Regime di interesse composto
Si ha quando gli interessi maturati si aggiungono al capitale diventando a loro volta fruttiferi.
Se gli interessi maturano una volta all’anno si parla di interesse composto discontinuo annuo, se maturano più volte all’anno si parla di interesse composto convertibile.
Montante nell’interesse composto discontinuo annuo (Cn)
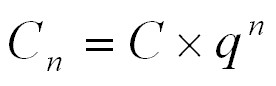
dove:
q=1 +r
n= numero di anni
Esercizio 3.
Una somma di 4.000 € viene depositata in banca per 4 anni. Calcolare a quanto ammonterà il deposito complessivo al termine del quadriennio che il tasso di interesse è pari al 2%.
C4 = 4.000 x (1,02)4 = 4.329,73 €
Montante nell’interesse composto convertibile
Cn = C x (1 + r/t)n x t
Con t viene indicato il numero di volte in cui gli interessi maturano in un anno (es. t=2 se convertibile semestrale; t=4 se convertibile trimestrale; t=12 se convertibile mensile).
Esercizio 4.
Calcolare il montante prodotto in 3 anni da un capitale di 8.000 € impiegato al saggio di interesse del 6% convertibile trimestrale.
t=4 C3 = 8.000 x (1 + 0,06/4) 3 X 4 = € 9.564,95
Sconto commerciale
Le banche nel calcolare lo sconto usano una formula semplificata (e meno rigorosa rispetto a quella derivata dall’interesse semplice e più vantaggiosa per loro) detta dello sconto commerciale. Tale formula può essere impiegata solo per questa operazione e per periodi limitati di tempo.
Sconto commerciale (Sc) = Vc x r x n
dove Vc = valore della cambiale da scontare
r = tasso di sconto bancario
n = n è il numero di mesi diviso 12 oppure il numero di giorni diviso 360 (anno commerciale)
Esercizio 5.
Calcolare il valore attuale di una cambiale di 6.000 € che scadrà fra 60 giorni (tasso di sconto bancario 10%).
Sc = 6.000 x 0,1 x 60/360 = 100 €
Valore attuale della cambiale = 6.000 – 100 = 5.900 €
Marco Salvaterra, laureato in Scienze agrarie presso la Facoltà di Agraria di Bologna, insegna Estimo ed Economia agraria all’Istituto Tecnico Agrario di Firenze. Curriculum vitae >>>